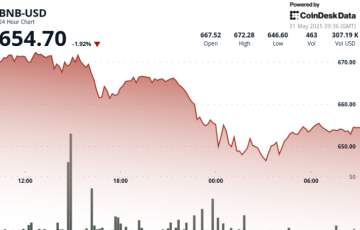
The result exhibits that the curved we obtained is an S-formed curve for infectious. M because the population measurement of a specific space. This end result seems to be an alarming situation for taking extra preventive measures to hamper the growing instances within the country. The curve grows exponentially from the early stage of infection within the country the infection begins spreading. The authors assumed that the people who recovered from the infection are still vulnerable. It means the those who recovered from infection throughout an epidemic has not developed immunity in opposition to it.

How to determine the average of the reproduction number for an epidemic disease dataset? The remainder of the paper is organised as follows. Next part illustrates Covid-19 open entry dataset, the parameters used for measuring the affect of an epidemic, and the strategy to identify the state of the epidemic. Table I depicts the first 10101010 entries of the dataset having different columns together with, affected person quantity, state affected person number, date announcement, age bracket, gender, detected city, detected district, detected state, state code, current status, notes, contacted from which affected person, nationality, transmission type, and status change date. On this section, we first illustrate an open access dataset of Covid-19 that we use in the remainder of the paper. Section III illustrates the mathematical fashions of the epidemic. India (https://www.pipihosa.com/2019/09/08/modern-technology-the-world-of-robotics-and-artificial-intelligence/). The dataset illustrates the element description of the patients contaminated from coronavirus.

∙ Algorithm for determine state of epidemic: Algorithm 1111 illustrates the steps concerned within the identification of the infected population within the different transmission state. 1 indicate that infection transmission is in State 2222. Additional, if the infection is transmitted from the first particular person to second individual and then to the third or the source is untraceable signifies the transmission State 3333. If the transmission state doesn’t belong to the above three, then the infection transmission State 4444 is reached. At State 4444, it is assumed that the complete inhabitants is equally more likely to be contaminated.

POSTSUBSCRIPT from vulnerable to infectious phase. Nonetheless, within the case of Endemic Equilibrium there all the time persists an infectious individual. R utilizing the differential equation, is to determine the equilibrium state of the SIR mannequin. A differential equation captures the progression of the illness. The Illness Free Equilibrium comes into the image when there isn’t any individual left with the infection in a specific area. × 100, represents percentage of inhabitants, which is infectious amongst the whole population in a selected area. It requires a continuing provide of prone individual to keep up the equilibrium. To seize the inhabitants change in a specific part, SIR mannequin adopts differential equations.

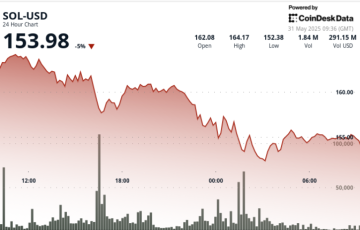
Prone Infectious (SI) mannequin. Aside from the SIR mannequin, they solely consider the prone and infectious population with out contemplating the recovered circumstances in a selected location. The authors assumed that the overall inhabitants in a selected space during epidemic breakout belongs both to vulnerable or infectious. ∙ SI mannequin on the given dataset: Fig. 10 illustrates the fraction of the infectious inhabitants for past 30303030 days of the epidemic (COVID-19) breakout in India.